Colors grouped
Colors separated
Symmetrical pairs
Mixed pairs
Same-color pairs
Symmetrical chains
Diagonal symmetrical pairs
Clan symmetry

COLORS GROUPED
Ochominoes has 24 tiles, with the colors assigned to tiles by how many little squares each dioct piece has attached to it. The colors divide into 0, 1, 2, 3, 4, 5 and 6 squares, giving 3 groups of 2 colors and 3 groups of 6. Separating and grouping of colors is a favorite theme. Here are a few color groupings. Finding such solutions is hard! Can you find one where the 8 holes are symmetrically arranged?

Here are a couple of very cool color-grouped solutions found by Adam Criswell, our staunch squire helping out at Ye Olde Gamery at the Maryland Renaissance Festival. The second one is especially handsome, containing both sticks and enclosing one color completely:

COLORS SEPARATED
Probably the most challenging solutions to find for Ochominoes is where no two of the same color touch. Here are a few samples wrestled into success by Dan Klarskov. He tells us that each solution took him two or three weeks! He had found solutions of the rectangle with the black sticks in many different positions without color separation, so he went back to see if the separation solutions were also possible. He conquered all the rectangles shown in the rulebook. Congratulations, Dan! No, we won't show them all here. Let's leave something for our other talented solvers out there, too.

SYMMETRICAL PAIRS
Another knotty problem asks you to form a maximum number of symmetrical 2x2 pairs. Certain pairs of tiles when joined can form a symmetrical unit. An exhaustive search showed that there are exactly 122 ways to join a pair of tiles symmetrically:

Can we form 12 symmetrical pairs simultaneously? Indeed, yes. Here's an example of 12 pairs, with no two pairs the same shape:

Interestingly, by rearranging the pairings, it's possible to make 7 congruent symmetrical pairs!

MIXED PAIRS
Another challenge to explore involves mixed pairs, where one piece by itself is symmetrical, and its partner is non-symmetrical, yet the two together are symmetrical. Since there are 12 symmetrical and 12 non-symmetrical tiles in an Ochominoes set, can 12 mixed pairs be formed? Well, no. An exhaustive search showed that one of the symmetrical tiles simply would not accept a non-symmetrical partner. The answer, then, is that 10 pairs are peaceably formed "mixed couples", and the last two pairs contain two symmetrical pieces and two non-symmetrical pieces, respectively. Here is one such solution:

Notice that the second row has two congruent pairs, and the bottom row has four congruent symmetries. The first pair in the first row is rotational. The two pairs on the right side are the non-mixed pairs, and by an unexpected coincidence are congruent as well. What is also remarkable is that the joint lines of all the mixed pairs are diagonal while their symmetries are vertical. Isn't that strange?

SAME-COLOR PAIRS
Yet another theme to investigate is same-color pairs. With even numbers of each color, can we form symmetrical pairs that are solid colors? Our best result so far is 8 solid pairs and 4 mixed couples, below. Can you do better?

SYMMETRICAL CHAINS
Now we can try to make a series of connected symmetrical pairs. Our best result to date is 23 tiles forming 22 symmetrical pairs, with just one tile left unintegrated. Symmetries can be in any direction: horizontal, vertical, diagonal, and rotational. All four occur in the figure below. Can you spot them all? Can you form a 24-piece snake with all adjacent tiles forming a symmetrical shape, or prove it impossible?

Problem solved! As of December 26, 2017, a non-existence proof has come from George Sicherman and his trusty program. So a 23-tile snake is the maximum possible, and it has millions of solutions, leaving some 24th piece languishing unpaired. Thanks, George, for clearing up this question. Some answers are just so... disappointing. Still, we're now going to hunt down all the pieces that could be the loner. Here's a start:

Update: By the time we finished this particular hunt, we found that exactly 9 of the 24 tiles can be the loner. Here they are:

DIAGONAL SYMMETRICAL PAIRS
The Ochominoes tiles can also be paired obliquely, and their symmetries form by rotation, not mirror. Our best result produced only 8 simultaneous rotational pairs, shown here. Can you do better? Strangely, no pair contains the same color. Notice also that each pair has an even number of squares between them.

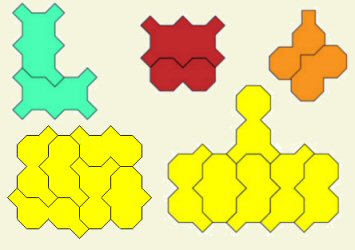
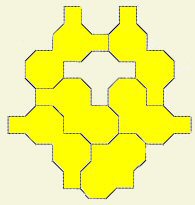
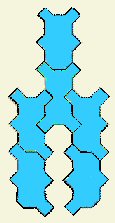
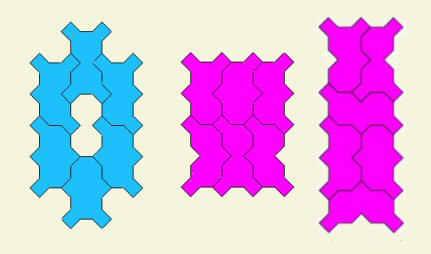
CLAN SYMMETRY
Here's another question: can each color group form a symmetrical shape joining all their members? Five of the six color groups can, indeed, do so. Only the two pieces with 5 squares are uncooperative; at best they can form an L shape. The 2, 3, and 4 squares, of six shapes each, are a lot of fun to explore and coax into a symmetrical formation. Here are a few samples. Can you find others? Send us your cool results.

For the 2021 JMM virtual art exhibition, we submitted an art poster and description titled The Combinatorial Diversity of the 24 order-2 Polyocts, showing some fancy color-separated symmetrical rectangles and the entire "clan" symmetry collection shown above and more. You can see the poster on page 2 of the description sheet. If you'd like to order a custom-printed and framed copy of the 22x34" poster ($49), email your request to Kadon Enterprises, Inc. or phone us at (410) 437-2163.